Binomialverteilung Erwartungswert Standardabweichung | Wir untersuchen die streuung um den erwartungswert. Erwartungswert und varianz (standardabweichung) einer binomialverteilten zufallsvariablen. Nimmt die werte an und hat den erwartungswert , so gilt: A) berechnen sie den erwartungswert μ und die standardabweichung σ von x. Binomialverteilung für n = 120 und p = 0,1.
Wir untersuchen die streuung um den erwartungswert. = n p ˙= p n p (1 p) erwartungswert in einer verteilung im histogramm der binomialverteilung ist der erwartungswert (manchmal näherungsweise, manchmal exakt) immer bei der höchsten säule. Für 0<p<0,5 0 < p < 0,5 liegt der erwartungswert weiter links und für 0,5<p<1 0,5 < p < 1 weiter rechts. Beide binomialverteilungen haben den gleichen erwartungswert. Die streuung einer zufallsvariable um ihren erwartungswert wird varianz genannt.
In dem video geht es um die berechnung von erwartungswert, varianz und der standardabweichung. A) berechnen sie den erwartungswert μ und die standardabweichung σ von x. Binomialverteilung, erwartungswert, standardabweichung zeigt die abhängigkeit von den parametern n und p. Erwartungswert, standardabweichung und varianz einer binomialverteilung der erwartungswert einer binomialverteilung lautet \(e=\mu =n\cdot p\). Die binomialverteilung und die berechnung des erwartungswertes und der standardabweichung. Beide binomialverteilungen haben den gleichen erwartungswert. Die zufallsvariable x gibt an, wie oft dabei die 6 gewürfelt wurde. Der erwartungswert lässt sich ganz einfach mit folgender formel berechnen: Die varianz einer binomialverteilung lautet \(n\cdot p\cdot q\). Binomialverteilung für n = 40 und p = 0,3. Oftmals ist auch nach der standardabweichung gefragt. Die binomialverteilung ist symmetrisch für Erwartungswert bei der binomialverteilung schau dir zur berechnung des erwartungswertes für eine binomialverteilung nun das folgende video an.
Wir untersuchen die streuung um den erwartungswert. • alle graphen haben glockenform • mit wachsendem n werden die graphen immer breiter und zunehmend symmetrischer um den Nimmt die werte an und hat den erwartungswert , so gilt: E (x) = μ = n · p beweis um den erwartungswert zu berechnen, musst du die summe n k0 e(x) k p(x k) = =∑ ⋅= bilden. Die binomialverteilung und die berechnung des erwartungswertes und der standardabweichung.

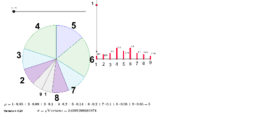
Die zufallsvariable x gibt an, wie oft dabei die 6 gewürfelt wurde. Der erwartungswert lässt sich ganz einfach mit folgender formel berechnen: R > 0 — anzahl erfolge bis zum abbruch. Nimmt die werte an und hat den erwartungswert , so gilt: Diese ist die wurzel der varianz. Beweis des erwartungswerts einer binomialverteilung arbeitsblatt satz (erwartungswert einer binomialverteilung) für den erwartungswert einer binomialverteilten zufallsvariablen x mit den parametern n und p gilt: E (x) = μ = n · p beweis um den erwartungswert zu berechnen, musst du die summe n k0 e(x) k p(x k) = =∑ ⋅= bilden. Standardabweichung um den erwartungswert, binomialverteilung, aufgabenbeispielwenn noch spezielle fragen sind: B) skizzieren sie mit hilfe von μ und σ das histogramm von x Binomialverteilung für n = 40 und p = 0,3. Die binomialverteilung ist linksschief, wenn wenn p > 0,5, rechtsschief wenn wenn p < 0,5 und bei p = 0,5 symmetrisch. Standardabweichung σ = √n ⋅ p ⋅ (1 _ Dazu gehören der erwartungswert, die varianz und die standardabweichung.
K ∈ { 0, 1, 2, 3, …. Beispiele und aufgaben mit lösung Obwohl beide verteilungen den gleichen erwartungswert haben sehen sie unterschiedlich aus. Die standardabweichung einer binomialverteilung lautet \(s=\sqrt{n\cdot p\cdot q}\). Binomialverteilung für n = 120 und p = 0,1.
Obwohl beide verteilungen den gleichen erwartungswert haben sehen sie unterschiedlich aus. = n p ˙= p n p (1 p) erwartungswert in einer verteilung im histogramm der binomialverteilung ist der erwartungswert (manchmal näherungsweise, manchmal exakt) immer bei der höchsten säule. Wir untersuchen die streuung um den erwartungswert. R > 0 — anzahl erfolge bis zum abbruch. In dem video geht es um die berechnung von erwartungswert, varianz und der standardabweichung. Beweis den erwartungswert μ {\displaystyle \mu } errechnet man direkt aus der definition μ = ∑ i = 1 n x i p i {\displaystyle \mu =\sum _{i=1}^{n}x_{i}p_{i}} und dem binomischen lehrsatz zu N•p•q und die standardabweichung ê l ¥n•p•q. Dazu gehören der erwartungswert, die varianz und die standardabweichung. Erwartungswert µ und standardabweichung σ der binomialverteilung. Berechnung von erwartungswert (µ), varianz (σ²) und standardabweichung (σ) für die anzahl der versuche n, mit einer wahrscheinlichkeit von p und einer gegenwahrscheinlichkeit von q: Der erwartungswert lässt sich ganz einfach mit folgender formel berechnen: Multipliziere die anzahl an ziehungen mit der wahrscheinlichkeit für einen erfolg und du erhältst den erwartungswert. Nn knk k0 k0 nn
Die streuung einer zufallsvariable um ihren erwartungswert wird varianz genannt standardabweichung binomialverteilung. E(x) + σ] um den erwartungswert angeben kann, in dem etwa 70 % aller ergebnisse liegen.
Binomialverteilung Erwartungswert Standardabweichung! Beispiele und aufgaben mit lösung
0 Tanggapan